 MohammedAmin.com
MohammedAmin.comSerious writing for
serious readers
Posted 1 March 2010. Updated 28 December 2019 to explain why it is my logo.

The Mandelbrot set is the set of all complex numbers that satisfy a particular computational requirement. The equations are explained in the Mandelbrot Set Wikipedia article which also has some images. I have adopted the Mandelbrot set as my logo.
On the web there are many pages showing the beauty of the set as it is calculated with higher and higher resolution. I like the following images of the whole Mandelbrot set at larger scales:
With the ability to record slide shows, there are also Mandelbrot zooms, which give the impression of diving into the set as it calculated with increasing resolution. My favourite Mandelbrot set zoom video is on YouTube and can be watched below.
It shows how as you expand the set, the same images recur at smaller and smaller levels of details, which is one of the defining characteristics of fractals. No matter how much you expand the set, you never get a simple sharp edge; it is always fuzzy.
If listen to the soundtrack, it also explains the Mandelbrot set quite well. There are also references in the soundtrack to other fractals such as the Sierpinski gasket.
In my professional career, from the ages of 27 to 59 I carried business cards for my firm and wrote letters on the firm's headed notepaper.
Accordingly, once I retired, I needed to design my own stationery, and wanted a logo.
Given my deep interest in mathematics, I was originally thinking of using the nine point circle as my logo. An example is below.
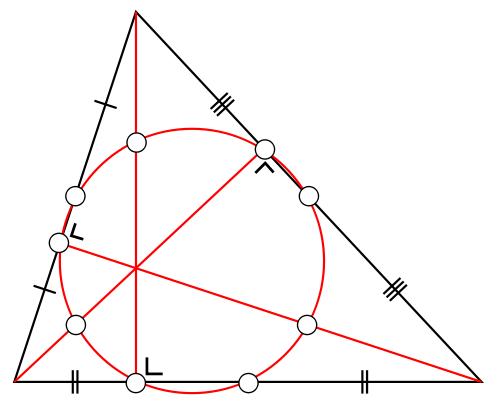
However I decided that, while mathematically interesting, it looked a bit anaemic. Then I realised that, as far as I was aware, nobody was using the Mandelbrot set, so I adopted it as my logo.
There are no copyright issues from using the Mandelbrot set itself. It is not the creation of any person, but an intrinsic part of the universe, existing from the beginning of time, and conceptually no different from a triangle or a circle, albeit somewhat more complex!
However images of the Mandelobrot set, once they are created, are the image creator's copyright. Accordingly, to be certain that the precise image I used was not subject to anyone else's future copyright claim, I used some software to create the Mandelbrot set on my computer screen, and then took a screenshot.
If you want to learn more about fractals, I recommend two books.
I read the first edition of this book in the late 1980s.
It explains in a very readable way the difference between chaotic systems (which are theoretically predictable and governed by deterministic equations) and randomness. The weather is theoretically completely predictable, but small differences and measurement errors multiply up over time.
Hence the saying about a butterfly flapping its wings in China leading to a typhoon elsewhere.
This is Mandelbrot's original masterpiece. It is very well written, but is quite a challenging book to read.
I would not recommend it unless you have studied mathematics to at least UK GCE A Level, and preferably first year undergraduate level.
Follow @Mohammed_Amin